The Volume of a Sphere (without Calculus)

This is the third and final post on the volume of a sphere. The other two can be accessed by the following links, “Coordinates in 3-Space” and “The Volume of a Sphere with Calculus” As the title suggests, this will be a derivation without the use of Calculus. This proof is Greek in origin, in particular it comes from a book written by Archimedes called “On the Sphere and Cylinder.” But the method of exhaustion which Archimedes used to prove the volume was later refined to Cavalieri’s Principle.

Theorem: Suppose two regions in 3-space (solids) are included between two parallel planes. If every plane parallel to these two planes intersects both regions in cross -section of equal area, then the two regions have equal volumes.

Okay, so suppose we have hemisphere of radius $R$ . Suppose also that we have a cylinder of height and radius $R$ . Finally suppose we cut a cone of height and radius $R$ from the cylinder and call the resulting shape $T$ ..

Consider a cross-section of $T$ at height $h$ . The result is a “washer” with inner radius $h$ and full radius of say, $r$ . Hence we can compute its area by $\pi r^2 - \pi h^2 = \pi (r^2-h^2)$ .Then if we consider the cross-section at the same height we have a radius of $r'$ . However by looking at the following picture,

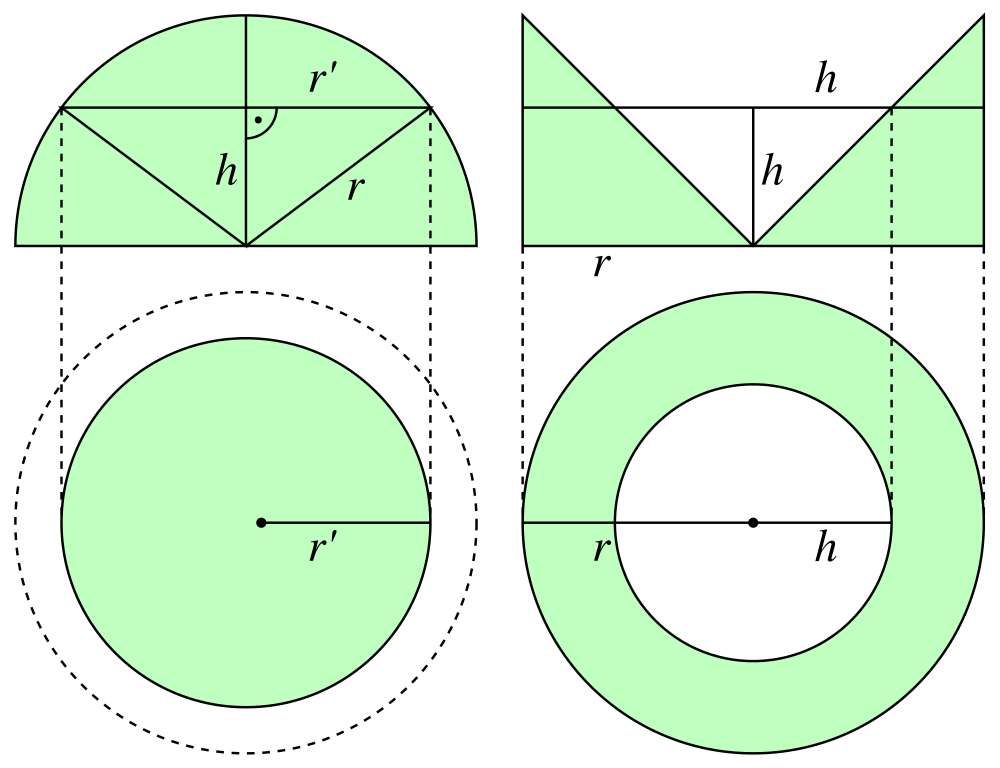
We see that in fact the Pythagorean Theorem tells us $r'^2 = r^2 - h^2$ . Therefore the area is $\pi r'^2 = \pi (r^2 - h^2)$ . By applying Cavalieri’s Principle we see that the volume of a hemisphere is the volume of cylinder minus the volume of a cone. Or $V = \pi r^3 - 1/3 \pi r^3 = 2/3 \pi r^3$ . Finally, we conclude the volume of a full sphere is $V = 4/3 \pi r^3$ .